valtozas1

A gázok állapotváltozását az állapotjelzők megváltozásából észlelhetjük. Az állapotjelzők közötti összefüggéseket a gáztörvények írják le.
Tökéletes gázokra felírható: p ˇV = m ˇR ˇT állapotegyenlet.  Az R a gáz anyagi minőségétől függő gázállandó, mértékegysége J/(kgK). Néhány gáz adatát a Gázok fizikai jellemzői című táblázatban találhatjuk.

line2

Izotermikus állapotváltozásról beszélünk ha a gáz állapot- változása állandó hőmérsékleten megy végbe (T = állandó). Ilyenkor a gáz nyomásának és térfogatának szorzata állandó. Matematikai megfogalmazásban pˇ V = állandó.
Két véges állapot között p1 ˇV1 = p2ˇ V2 (Boyle-Mariotte-törvény),
a V kitevője l, ezért a p -V görbe egyenlő oldalú hiperbola. .
Izotermikus kompresszió csak akkor érhető el, ha olyan lassan megy végbe a kompresszió, hogy a keletkezett hőt a környezet fel tudja venni, vagy a gázt olyan mértékig hűtjűk, hogy hőmérséklete ne változzon.
elore10.line2.

Állandó nyomáson megy végbe az izobár állapotváltozás,
p = állandó. Ebben az esetben a változás V/T = állandó
vagyis V1/T1 = V2/T2 törvénnyel írható le, (Gay-Lussac I. törvénye).A V kitevője 0, ezért a p-V diagram egy vízszintes egyenes. A lap elejéreline2

Izochor állapotváltozás esetén a gázok állapotváltozása állandó    térfogat mellett megy végbe, V = állandó.
A folyamat p/T = állandó alakban írható le, vagyis az 1. és 2. állapotok esetében: p1/T1 = p2/T2 (Gay-Lussac II. törvénye).
A  p-V diagram egy függőleges egyenes.A lap elejére.line2.
Adiabatikus állapotváltozásról beszélünk ha a tökéletes gáz állapotváltozása a környezettől termikusan elszigetelt térben megy végbe ( DQ=0).
Mivel a rendszer és a környezete között nincs hőcsere, a sűrítési munka a gáz belső energiáját növeli, ezért a gáz felmelegszik, expanzió során pedig csökken a gáz belső energiája, ezért lehül. Az adiabatikus állapotváltozás törvénye: p ˇVk = állandó. Két állapot között tehát p1ˇ V1k = p2 ˇV2k ,
ahol a k (kappa) az adiabatikus állapotváltozási kitevő (fajhő viszony), az állandó nyomáson vett fajhő (cp) és az állandó térfogaton vett fajhő (cv) hányadosa, k = cp/cv.
A V kitevője k > 1, a p-V diagram az izotermánál meredekebb hiperbolaA lap elejére.line2.
Politropikus állapotváltozás  A valóságos gépekben sem az izoterm sem az adiabatikus állapotváltozás nem valósítható meg tökéletesen, mert a hűtés tökéletlensége miatt a hőmérséklet nem marad állandó, a hőszigetelés hatásfoka is korlátozott. A gyakorlatban lejátszódó változások ezért a két folyamat közé esnek, az ilyen állapotváltozásokat nevezzük politropikusnak. Ennek egyenlete:
p ˇVn = állandó, vagyis p1 ˇV1n = p2 ˇV2n,
ahol az n politropikus kitevő, értéke k és l közé esik ,a V kitevője
n= (1<n<k),
a p-V diagram az izoterma és az adiabata között futó hiperbola.A lap elejére.line2.
osszefog.  Összefoglalásként hasonlítsuk össze az állapotváltozásokat grafikusan. A műszaki gyakorlatban előnyösen használjuk az állapotváltozások ábrázolására a nyomás-térfogat (p-V) görbéket. Az egyes állapotváltozások a nyomás és térfogat különböző hatványaival kifejezhetők, csak a térfogat kitevőiben különböznek egymástól.
allv652.
Megtekinti az animációt?

allapd3.

Izoterm állapotváltozásnál p ˇV = állandó,
a V kitevője l, ezért a görbe egyenlő oldalú hiperbola.
Izobár állapotváltozásnál p = állandó,
a V kitevője 0, ezért a diagram egy vízszintes egyenes.
Izochor állapotváltozásnál V = állandó,
ezért a diagram egy függőleges egyenes.
Adiabatikus állapotváltozásnál p ˇVk = állandó,
a V kitevője k > 1, a diagram az izotermánál meredekebb hiperbola.
Politropikus állapotváltozásnál   p ˇVn = állandó,
a V kitevője n= (1<n<k),
a diagram az izoterma és az adiabata között futó hiperbola.
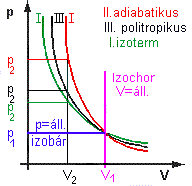
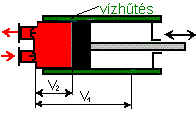
Az  ábrán vázolt dugattyús sűrítő V1 térfogatában p1 kezdő nyomásról indulva az állandó m tömegű gáz térfogatát V2-re csökkentjük. Különböző állapotváltozások esetén a p2 nyomást a diagramról olvashatjuk le. Azt tapasztaljuk, hogy a V2 térfogaton az izoterm állapotváltozás esetén legkisebb a nyomás, és adiabatikus esetben a legnagyobb, vagyis adiabatikus kompresszióval nagyobb nyomás érhető el, de közben a gáz felmelegszik. Politropikus változáskor a kettő közötti nyomás alakul. ki.line2.
1.-2. mintafeladat  3. összetett feladat
A lap elejére.
A lap elejére
A nyitó lapra Gázok tulajdonságai Tartalomra. Berendezésekre. Keresés.
Nyitólap
Előző
Tartalom
Követő
Keresés